Last Week’s Work Review#
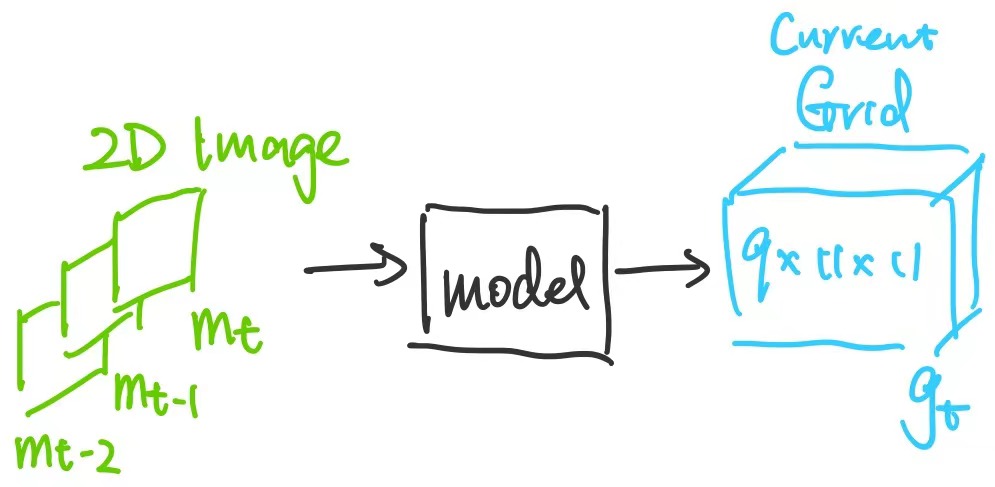
Recall our Phase 1 visual module training scheme
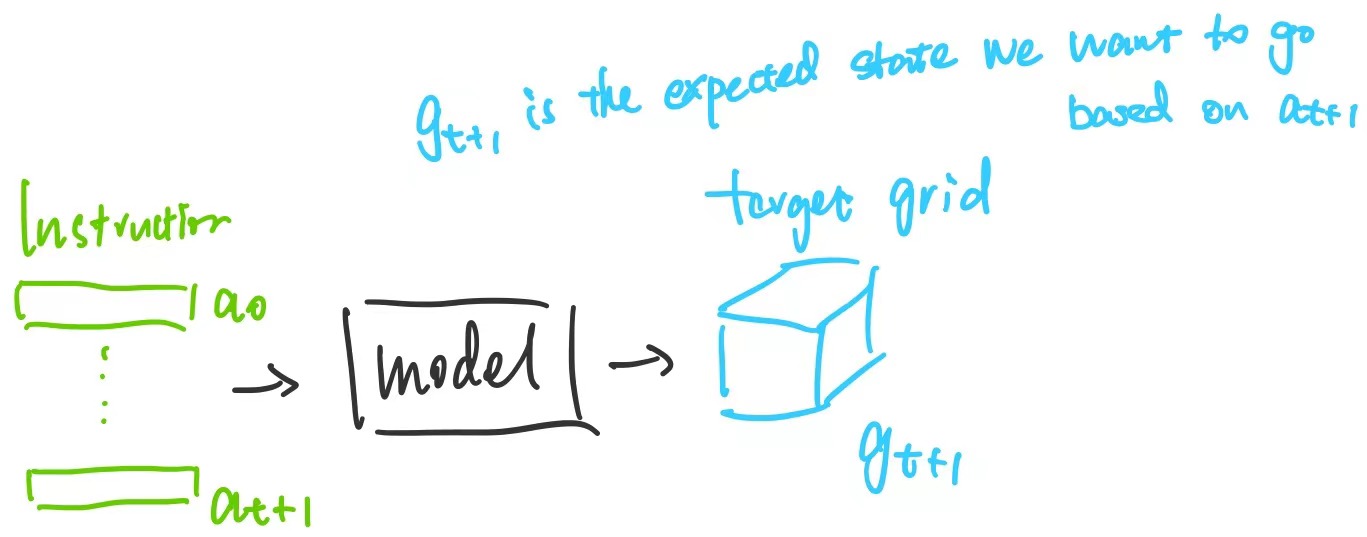
Our Phase 2 language module training scheme
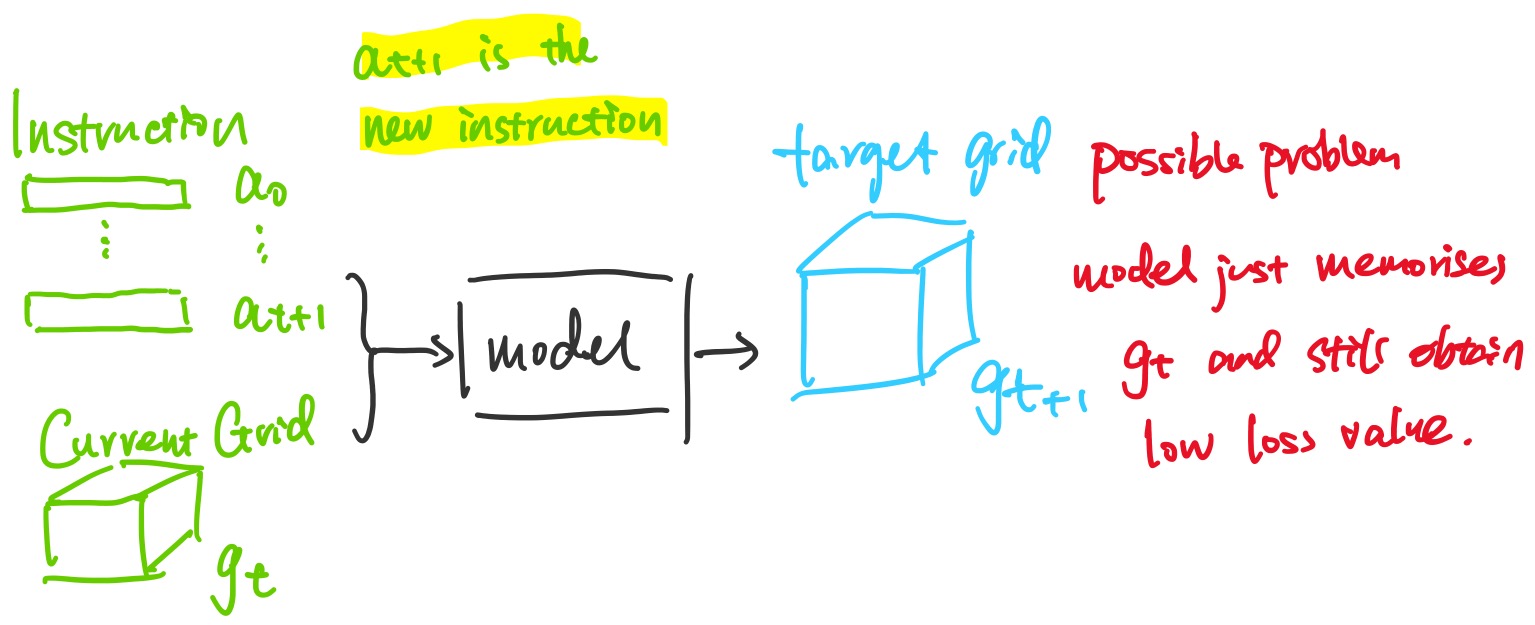
the testing accuracy could achieve $99.0%$ But I doubt about the true performance of this model.
- the model can achieve high accuracy by just memorising the current 3D grid value as long as the incremental change is small.
- which is true for this dataset because one instruction is often paired with a small change in the environment
- I should change the current training scheme to prevent model from taking shortcuts
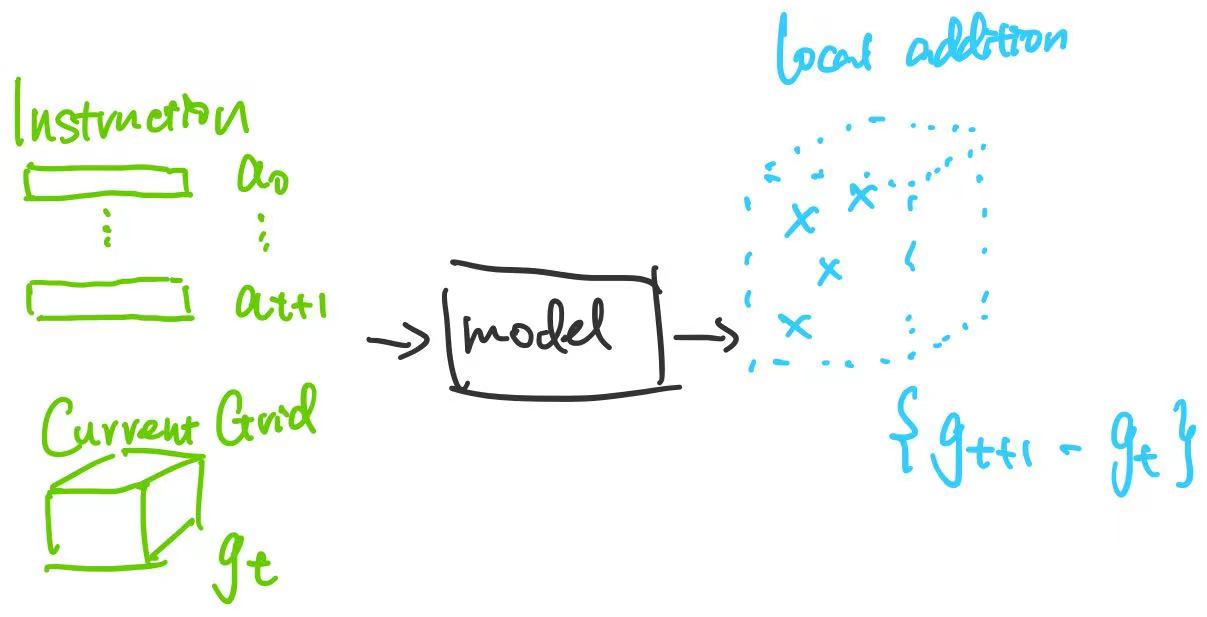
- local addition
- one step (no intermediate states)
- local addition
After completing language module, our next step is to build PDDL model to bridge the gap between current state to the target state described by the instruction.
You need password to access to the content, go to Slack *#phdsukai to find more.
Part of this article is encrypted with password:
2KL193ngiqg12yJiDH4bw+D2Nlm45qLF/v/qafJrxuBWcpeaKoACuOYOWAlIK5SiIofGzwRhcZOhHR3LtmKaM/j9J0y2vO9Z69ZqP4Ko3UkGLexL1+U7O0+yKZZB9Dw0NBdkewbMFlw00vKHbhtiw37xANvtixAYOeEERG9wDEZPCufYK0nH6DvqP7pzJh28eiAW5I5gKKaMPGGAslvygAU14z7zdpsqrXwajbgmt8F+Z/ivDwgux9KSFtt1azUe/G3LtXjZ2DV98FWXTX9rYA6yqvYFypTnAozyRodTgJ6XJ632eaBg0AYilHlCmk/mZLmoXiPfhenzNEoWOuuTlCv8rDB5x7P1Md5eWduAPPmyEmg3wRZ1vjkDARmudu1M1zczgQnsPwhM3TcMGHb50RGdL9KvqJT82X3e5I9wpBM6VmQ62/jq4X8FtREkU3SUcu8LST9htrkZzBnsLfvMts/VZriOclfCb9mDXuO3sJhixVdf1ygPrIQ3dEGkpAA1kWw1FF5EqJQynVAWOGNURUoKQjNB7FZzM+slz1TmWtZhEvLWDuOBhQWLp4zX9knz5eJ+Q1ZgMfljPEEkrVIcqDokag0kJT5eo0Pj8zUI0gPEAA5KYD0SzGwDuqbfJp6I3VIqZWm1xxpa4L4PhUvK05/av4pQAd14eOZkDP4Uliq+1fWS6aBoKtqvh/kafeVFFFpkahp+Zk5zsJUUvSRg56Ravg0SX39DZk8W1dt5b7vsd6+321tBWjDsmh7qT+cunQsYXVfJNv4AtQdWybA1sh4awn3OCsOsAXjnXx4wi0PVYz8DU6u/yZtHdRiS4Tfq7hB5hOq8QsatTEwo6J0DQSgc2QeVeyrPWRcYGJxt/y1vaxrJDdP+APPrvH+iN5sK+RIWLreOwfd9vO8aQwuWmWae5VacUZSwTkkbBfI0wMzvFfqcn1GfBo/3eQLUf+M/L3hgOxKbH9dQSf6BN0Z1klp8zrUzkd/49OCp/Z7ZAKn5UmiDtD02lWAMF+N1bjOU8ZToLYsoEWjtepbC7qQWhd2n7V3qbNoiEOdnXK4txiAvlYm9Sb+yWoQxM4ByfB25kWkRBMXhtCbZXwUTauZKk0r1XWyxA6Ew8qnW1V+X0Z1mP9fHOFNJz6pI/DHYdLqyq4diac2WZ0N8vlhmJlNbOGTUgxtR6FiIk6xIAabu/f6j9FxAhw3a3uMDdYWMaegQTTI4FklQc90p2Becw1/DPo9EPRQgREFJhuNnBlqE4TjNVrwzvy+4HFLtUsk5sYQm7LT0OXwB0pP4Nxmohs47dqo96l6biD+Q0pJ7xLMNB5fz/1YNk+1nhwrpGwu7QON1rXlH3oFaJJD7PVvjQuVSlwMoaTWaNuQijABD5fK8Un5xN2r/wAZm6NDKoWtdCu5tn+Y3EAq3Ho4VRLGRpem7/jaHWu8UXPDA4BrAqq1E7VF+5wwVFt8B9X3yTYSmrtKSFyUY/lh15aWDP27/BkHnAA1xDXi6Y9rHF+5M3Q+2q1e++qnXS0J5jHk8wU7EFldEF/yGPOAH7eKtgOFgWgnkSbgazhOSbpj76olKeSBJ2oGcuaCwKXb0nD+pN0fHqQLU2GA8oqbZsrYTzYqnmC52TaswabjpOYkX9g+F4ReuwxM+Fy9EcGOMUzz/UL8pUfKlllEG3BF+dVBhC/maNVJfxikrBXcUmhTlSW8w7n2elNQIATLAoiOcNUH3SYg/taJUAdZFnsJgyWY8awnsJA9QETGroJnh6x2xHZr81O19Nl8a515q+8AqR5IR8JhtGvv9Tw9KFvhZ9elGFPnDZ+BLW2wXUTQul9ZM1rDQZcK+zKfgXiUuElqoKnV8SlqYY1YCfvCMRuii9q1HjhAK0kxqF5wQI5bZ8QGodJS+ztWu/m5zXtLaig7cDqqh04jC42B/VuzpJ2mCe7RpFgsF0ZFvGeUSyhdLPgpUU9xSZRBNQPnIk3bsOMU10wHsa4tsdtOvk0W6cfb25gUK6+J3DdG346qgFYH8JvtcSUoN/hK2Gsa6NOuUP2+Wzw9EkOqQ/OI0WXq2yWiyx0JPhM2oiODEtg0oDfZzCT22O2RI74e0tXUfJKHNODUdo2zdVQCAcVmDVQ/TM+F1+w29scq0beDvKtyuS62Z4u09VDV8GznnAux8Th+Ab2gNmnksHRU0msPXkdEJRavIDXG0TFdyggUhUCXfRMNUa1JOAB5N9x0UZSX9gBZ8Df3BCr9fKSXmafveHxGPp3tP2Cv9OG0zRBEvZr/vNQeuV9fJ1ZTTRPSirc0MPVrif6pZgQtK7pGDzz4k22oty0D/DyyWtoC9snJB2WdVEbu6yjfufQ+06W72447gHOAZslrv5Dcu2ZVXSjRmMC97vlK00ib8vPZb7PyB64wFY1o3mhApXorByVkoF58gLqJanUkDaoNA4hmRvHce3/lox9CgYs6N0R0e5gghLeBRShnRpJQWRnuREExOnZjqFve1Ll7bjzOVCW1uWlgEx1RWhcoFRswv6YWoFuEuuYpo+uroVnHCYA4oR9gYbtckLgr1xY1O3UhBgcMgoOGvMx0Fp2FyKh4trBimQEcEdYPyTmldyIoHAoVoS43UA9HYCUqzIwG2657LerPiB0cXrE49HeUm7JHVlghSJbRfALqNtETvq1tAnbq/Ngb2YXNN4QpH3RQenmfGsKuv2R9uROt4El3IjzgLxliPXKexzqM97bNm9YWOzjH2Fl3pHYHIP9694Nt6QwFACmlwy89pXhq0V0kqHFmu+On7BdB8tBDUn3y0Cnom7Rb+dYNPPfpSZ8s7mLznWCbwVEqRO3zfMl5jcFLGLJshElAr13lAYGA2VdCTT/DiIs/fHM9OcJFog1bglHgRWvd1TC2FHEqBMM0dy8UGg1GuLoVFCRndZ/GKRm/fYZjM8DMFNyH4OIFMpDFezJHO8flxGKMDXpcpF7axrYsl4UGauj4Jb4MSNHY+vH44u96pZdibhCrY/tTwCWBkxswxVXsW21czutXdFo4aLRFDfi/6i4NhOZUJTwDfLceW9beZsg6ZdSBGCouOtFCj+QRSUN/K/5AqqtVU0JUX3ZXjOJKUCtXUzn74UoAqZVVtuczdaIprdhmA7urfHRTPliBjhKDorvU9gx2el3kIDIDWLvkm/xlSVFuJFG6Pd3kRk9GeblILLxwoJ4tK4laXKS7kCh/0LUzpsKC4dpKzj266jnLDG2fPaWX2rk52wy5/iTiuq7F7pjl7fhVD0xVy8OV0p5FAldif7E79vk9ny32SFaaTtsGBb/lg0XzqjpRhLjR+7SUGKKtlrwtesj7wKrSEF0KQKovfxfsFLka2+qBUwqJc7ip83qDP9npyZadb5hmhcQOyQIwixNgtQPgZUMJN9oQOj0AzK7I0se0f4ZwSlQNJSuRqBzzNFo+z5C1rRINbwqFP3mRTvIBE8SkvIwFHLPcoi7rkU5nJ7dlgDqbwrxGKmOrqWo9o4t1YsgxUy0zUqk48RG5zq0lW3VajF2JkH4fSM9AUDdF8Z+Xoxt/NXD5Qqx6L9JdNZ7z0VF2AlJr4iSrdDwgzdzhY8SVt8H45iV+sVVGLkH+RdKQNfvWYbyQmfTjqEmVeFpSqoAi32fs4HOQ7QcRT+QA7f7ryotrXE1s+h0ONgRSaX+2zxPLgq6+QZW/GZXVtAWISkRVyKLwlZGwVvqOpon9pOQQ4rKl4IhplbIMwvP7QhDbN2+PjA7jaERFgubG6Ci8IUckiwOTsji1YjP93xj7mmXBYDWz34E/FSd7KQOoLXKxBHkUvy+fJh/sXbb/lOOqfYagIcYZwQrxlXmwvcxJYqZu5saVo9KQjmCUqEHTNw9br3RTH5MMohTxzR03beVP6HEh0mMSEOAeUJAPPcSqnblt/wltwk2eA6aTuoyFyRVAvR0ECiX56fzuHwCYURWEjzxkc1RFzouTq7SKZ/bROK9d22QgEGmvIzAYMkhw2xAYFv/7Ve28uLrNdryUAAoTUdw0wobekaasU3tgfIGCZ7JWGxRrwzNPq0r/3ezXDG1qU53th8eWCH6Qtxb1L12ldEFYId0UGx3iYQKRUou/xuT5gwu6J/IaitWXgdmf5ZRrKsOXJjf8SIjdGCdmy/Q82UGHSyXNh116xHzjXgDWcbYHhd2sKUrgbZaCyycc/bZC4NRXDtRx8eIDf5Q/DhKY9zmld4jPR9EgrzPdYT71aFJj2cP9Z7phJCC3E6UofQPjRQzSlBIC2d5+7+0MgU/DdAOauCm725MU3UpTT74p7gAQPNza64LgeW66aoi0ciQRgN3r1RS41VvOpjb1fIXasjJNzHmLA67/KZI9YJaXgGUK04DIuJijLqqIUudQxyy54NSoMS3Wjvy4wqExZPPk0vbKr7omFODerlFMHI4oCwpH6dkVgSnlc/jUL9t7ta5DunX4xgrYfwM21lUVSqFA0HAc/bHMOQO8JEt9wqy0nij8zpPyG2TKSYZAIveF55q4jupFl2CQ1xv/YjOkhMYW5AmZszWq4ml5WLnG+uMs85x40+mg9J9vqg1baT181/rLmjl2h2OaMQ8gsb/pHFvFSCLe10r9KlpggmcdEPQ8uEAZpD2wjyqTmYTQqG44UmU61jTz2p7+jySZiB7txjgeL1AdR0QAIeW0Y2PkAZmaVJXAp2hXytVgQzMsEUHXLeV7+67LmmAFi0JyhxQ33lCnTjhfdYXVTrwE9iTJmRIOn0O6cPTcg3nBZPtEM7e9aHDfhBKcV0MZTiRoq1o+tk4H80/cqsu7ajtOFzaTSFRwG7ffd+e4dwwumpjVXc81txr4H5KiTxH+Uw1szsNgiJjLYj7VpYha/lgaIbcwO/NtRffVzxFHxkQfXNSnRMPZfLFN/N5FIpZoFbb818K9LM9yw6V8G7qdY/qFrOxdK/Dxhl8FbAWeNvqaR6hL+yIV4Thpm40gNFVm2M75Q33e6EvJ58NkDDqx5WJxOVVvVCh/n2WYMqDwjS+5VnNiCOc93J0jPa5NZI0LST/QMwk2Ii6ervfzceEGhSI5ow8kHQiJ/5YO7C+Xm2USgaPWxIxkUDt3AFT7Cm6ZezPVXnkFZJvbxzF9u3+nAQ9BUksTBssdAgPolQsxdBZmdt5XkpFMScyVOpAt7+PdRydQqG2ZZU7Fa4RH00EKyM6Cu0kW9hIalNjVPRaaIwMAPGgROBhO8uF85FcYz5iScoQ6KYK7X+aIIH7ETuSM/hTWfK388tBM6uscU/wfLcl8wQcewkD8gWCUCEs004UDiiwqhE4jPcXPWZPegTGCsJUPQm/8KdzZ0wC4V9amiZcfg/fntm+MskUiRAIhDRmmQF4ZS86TpoXCW4+SxUW9n5Gv++Rh0uTRJQ8qKvH6SmERes0LNAmt1rzqUICqoRiKzgTacb1IbW/3q0v7Q+LqHvH4uWAUvvtzEPScDt0Qfor1yWiFZHoly4BTfuZU+pDV9Vli6bgKrspyL8RFfLA5FDGPc8dL4YQmUNsjs7rGIDU8oFC4Rc/AQCKW3c6eJF2cwiW+4G1h2KIPz8Ofmg85By6Gooqc/wCchYItmoPm9+s229LfSNZWns6EcPBACjy8rHBTC1/1yXUSsh90b81XJJp7Ut1mHtUjD8zHBK0VYe35QSfhwXMAyMlaSerIf5AHr0XpiltOt4pRZyzUOOvLrZkTAi2ug8NJ88a+Tyz3/D6rizlUrcJQlWkqzX4IpbE/OiCfAjPFkwjyM6+9ZCyXVbYF1WOKEMKZTsAL1omoPA/PaqRfei3Gey0eQcZwAGHphYBAvoY6+roXhJg/GXd7JympsOjTKPvcmPo7B5C+W2vhqqR9m37pXi1iZ0WrM1y3vnWbQZGb8p9mCEM+z4tz/BypFtWrsVfgBXt1MDPvJXJYg1fgRY+Sr8x0gWi6w8ReWn4flxiRXxQe1Nl9Ox1levjnVfVdWXl1ALqnwDFlaEwO1yrJazTCRW+XJapTQzIQWYjoDzupiU3ixDJR2Barzx/ydZEDQwKRb9WLxsna+tgsUP5PQIAzC2ROXItADDHcN23/NUO1tQJoPasH7jvDCKMZp7VYW68tuvGK2Q/pRz6FDPa0a04Bvy7kSvny+Lll5efuDdGRHI6GjhZCMcAQmC3ZeU42Rm5sMJfMu2My1hauliXVBCNnrwgVows0RlN7d6W8hu0mI3JYlVqjhDQv01nmHNsoIr0Ty0Bava0pOX9BdMtIDyLWz+snflJInbFyy4j+vpvnBBxFhiCnevK7CwbHU6wAZr46+6M3ELwnYfQ/y9PY4XZmJzGJsjzTmjw7G+/3Gfnm9k0V3ZSAJv4G/J0UPGhku5op4KrPi4lZj2rBDie3PuvTlixGxKFmBM+GRBGwKXBIsNFy2q5GO3E/g9jb+fTtPXq7XUAWHkKmo+pEyIv3ChDXl3zQB/x42xMQK5rvyz7Gu6PMe50/nFJtMb2m61PkSzEIyC+e3Q10Z3EDEBeoQuTWnubNeILqoedoN6koPE3yxWVbTiY3+NAs5HD45ohmVY8JNdgBPM7c4VfVd22zs7OMndrA5qN1dIvXZ2/txegyJiDHhY4L9sc32F+aW/Oq5hW6oX4hqHepmk6eXbiDywpVQXdegGXiVrpovs4ukt5KWIjlVReFkYYvA1Mb1SL8Tzu67wAVLEzCwnxkeynedcWM59Z1NJ6+sj2A/k+N7inIFOEWXNep1zgry/VDaG2DEB8AJ0ZIqynEiZSUNPvb+unheqTf+VjudsdZhT0yD5BZlXYnQ/jgWue8bALqPfEMyh0dwnKFnaNGcfEcu2cYiKgQ0sVtoDiQl6376dBkRDtWcpu9zJoTJGsqKVtZyOoR2BH7nNbChkx7Ka5yNG2siDqCt2om+ye74KqSDGd41V6qw4BxpOTT4JTaQFofFCM973VpBTur3SmRYk+JDANxuiElRDg12E832CFY4+dQSZjUU+JQnepL4RBNRbufkmkGyyEVLNtl07TwF9AbkYPGv2J1rK0W0SXZ4YvF3zVu+cZxsDKUtLzCvjdrX3iI46n14TAxwhsUNsV5TjiG4CFZopYyGOqFuOyiYDZa4iWfohPQSlDW6/LXBqTI6JZwMPnXlki+ghxJNhuXX2Y94WhzlZz4hpZ1nInEPgnwviPBscmDgFC/aFddFXmqxniy6NFnKSFF3MrYUMm99MOfdkK2DaXXXV4gSvxqtzj7bAqKosE3R+zmA/zJ1v+1kTAkGoGIcWrV8qLHwdgLOeVYfpSl2r7IV6HgrpDKiCSMEduxic/Xe12rYD7MqX5olTFrkzDGHUXDX3V3/pVV9uXMzmmvw2WI+7mG4TGtBc1CpRsMzVnm9iyQRig8IFTcmoGNJd8uxlQEL338PiPJTmF/hk4nimUYv3QDSf8ZHsg33dHVIKkWAjRrJGb5J6UXAdXiUTeJj+i+W6lJLZoqBcDmK3GCHblPdSLIkQxwqo+DQBZ5id3EI1CBJBAYjvK6Hhyhc3MnKxTKm3xqlki5dF2fbfv7HGXzYzVmhBZ/hLKP1ti9sQ+iIUQwXmNaXOnpL4ODO/ocjmub6SBRNcI6O5rqd/C5YAyvC1UokYBH5P+G6LyokL4qkatQLgZvundJRufCqVuF4xwi3+PWhEFQfndnHLMxmDQOSfY25buugBsYUhFbjbmylWeKmW5p03Wzjsvv7L1Z4Pg/F/HlvZ5jckJUgi3lzJWPBJwNc7dIcoIhAmZUZ9gQLU4nBqUePFsWfO+jSPY/4g3/z/SljnedpBZ0Kx/2j925UeeMUSBRgv9jXXkLLfEd8u4di8uEiSboxibjqUfyvwqXp6wrNrGYpEFu4OYCQYT6WX35BjHU6ASkrbQC37AMftZkIaT+YM53IvSxCkNJ6f9MePT/4yfa2TChRAev8KRYXQQezUD0Z0FPTEok+mncerFhuh+kMqXk9MIffJlNneZ4iFOFiQ8KFUbJtdUNGkEXCjFmNprc1KNmR/GSJGR5+y0kcsY9f4YcdN/PSmjg/SXk5+CeF949aOOTynkFcMLlOtF9bgTNMYqlbjxvluXynbyJW2yMTeBVLqIIqqboVkbVHU32FDQK5H+rYaFA/QMV4CO59nPyzpHuGGoA+o2cYRLQGJn2rsqUMjAlu0xzoJP487yrxIsi3nQYxhDKy95oQh+7UouBh8WF0sH/hRoGjB9nLoWTXQjqLHXjyGOyCptQxjdBn4SMvl6BJV89d04lpMITst0kCDIp5OjvLO6qYI4a8cMGSdXvUPw72fptiYCplrdhdKnYKchpPLeb4fdgNZB1srHLKt6aU8U2GaqaGTkogcdiKCp2Of4DwK703vPeyJs1KpU8Z44/yXQIn5nqW1EWOox+aMmgJ4xyn0YNslQZFSaHVUR7biMEQsc1ljeSROVyex2uGRrL7arOLQpt+fxZKqmaea/3dwyZrgV5XQMgsV1HjpwiVBqFpQquihfzzwjPsOBH9KuTAstRzpzs1m7NfcrGrP3IuAEkC4/kKs3L3nHMQQfZiXuhm2FsDAtrKcihuItlhKpCDzqcdPbZBjxCLaQ4O7/haCwvel04AW1XgSzzVGsvyUBOIoyAVERB1bLBMm6N4DWYjpOkgzQU9fxvO4kdremfvXP4PvBgpv9hFVchdGux4iy4h3cACCKojx92CNkJ4S0TuLxfFr27l6JdalLrPHcbEdO2HCD1ArSWPTcksbo1UZk835tr3imGavxfJADh6vLtnq287BitPo8owYB71FDDz9D8QMIpoQwtuC4ik4IU4yEPc9DeuXDBW7VylY+kfL5bQq5PPCU+zw4FpWQr8OBGTX0x1n1HuKapcYvPeq2kmgnCnFJCTu2MBLkVyh85CyOpFql2mv7zshuT4Nt+TMrd/oaFXd9rM+lKs+PXXo9ZwIoeLJkVtO9DUq5W8Q88kJ3oYWOczhR5oy6JerISrfIgS9Em5BHm0Z6pGDf1+RjWF6jrS+C3fZ2lPLNAliv1Um0tXgY9M/lnUnXq6RwsRMoYgN12BFpt+fDDCRCxh0sdBnPDFincB4Xn/XIS9I+XXt0wpW3VvcfJkBM40xXis03FC8f4EedjtXj6zvfBUt8e/3ANb1fTNUKjeWQuQxgYApLBoW80mElTzQnfkbjlF7nnNXkrdxe6dSf+cikIrWRGU7Sope9JUXnchZR9X8vS+EdZutAsdQ0ALBsO8+NrtAklSC4c9hW63zAa9Xpjmkg24xChsZGkum7zcp8h6cd5W8/YedyrAI3u7XtAOSn1OL/epbBCA+cI7MYnICKb0t9U5eEXfrGSP4PsfOMW+vDFRKAku5MjN4xDHaWW1Api/bByqmw+SNOi7fvmb3H+oK7DvkVt+LvxFWXpvM1GyJgUOGzeEfx5G1uBSymtF5pt5VRisozbjq3Hn59ODB79zhKqst6FJiWzuS3DP52/pCtHYrDSGoX8cKDfozDIjGXoSpLFKuc407lSivgYI9CsJMP3eS5VVzM7RlPZmftW+PAsyDggUFxTGb1+i