[TOC]
- Title: Failure Modes of Learning Reward Models for LLMs and other Sequence Models
- Author: Silviu Pitis
- Publish Year: ICML workshop 2023
- Review Date: Fri, May 10, 2024
- url: https://openreview.net/forum?id=NjOoxFRZA4¬eId=niZsZfTPPt
Summary of paper

C3. Preference cannot represented as numbers

M1. rationality level of human preference
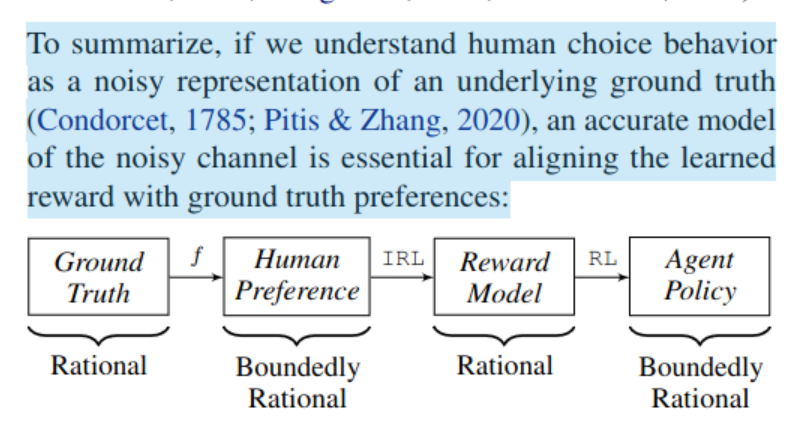
3.2, if the condition/context changes, the preference may change rapidly, and this cannot reflect on the reward machine

A2. Preference should be expressed with respect to state-policy pairs, rather than just outcomes
- A state-policy pair includes both the current state of the system and the strategy (policy) being employed. This approach avoids the complication of unresolved stochasticity (randomness that hasn’t yet been resolved), focusing instead on scenarios where the outcomes of policies are already known.
Example with Texas Hold’em: The author uses an example from poker to illustrate these concepts. In the example, a player holding a weaker hand (72o) wins against a stronger hand (AA) after both commit to large bets pre-flop. Traditional reward modeling would prefer the successful trajectory of the weaker hand due to the positive outcome. However, a rational analysis (ignoring stochastic outcomes) would prefer the decision-making associated with the stronger hand (AA), even though it lost, as it’s typically the better strategy.
Preference Ambiguity in LLM Tool Usage: When applying these concepts to large language models (LLMs), similar ambiguities arise. Should a model prefer trajectories where a risky action led to a correct outcome, or should it also consider what might have gone wrong (counterfactuals)?
3.3. Reward misgeneralization
- we may face cases where different reward function can explain the agent behaviour in IRL, and we cannot tell which reward function is the true one
- the limitation of training data will cause the reward model to perform poorly when exposed to examples that are out-of-distribution (OOD)
- again, it is a issue on how to use exact number to represent the strength of preference
