James_queeney Generalized Proximal Policy Optimisation With Sample Reuse 2021

[TOC]

Summary of paper

it is critical for data-driven reinforcement learning methods to be both stable and sample efficient. On-policy methods typically generate reliable policy improvement throughout training, while off-policy methods make more efficient use of data through sample reuse.

in this work, we combine the theoretically supported stability benefits of on-policy algorithms with the sample efficiency of off-policy algorithms.
We develop policy improvement guarantees that are suitable for off-policy setting, and connect these bounds to the clipping mechanism used in PPO
this motivate an off-policy version of the popular algorithm that we call GePPO.
we demonstrate both theoretically and empirically that our algorithm delivers improved performance by effectively balancing the competing goals of stability and sample efficiency

sample complexity

Represents the number of training-samples that it needs in order to successfully learn a target function.

PPO theoretical guarantee

the method is motivated by a lower bound on the expected performance loss at every update, which can be approximated using sample generated by the current policy.
the theoretically supported stability of these methods is very attractive but need for on-policy data and the high-variance nature of reinforcement learning often require significant data to be collected between every update, resulting in high sample complexity and slow learning

reuse samples

allow data to be reused to calculate multiple policy updates
but also causes the distribution of data to shift away from the distribution generated by the current policy.
this distribution shift invalidates the standard performance guarantees used in on-policy methods, and can lead to instability in the training process.
popular off-policy algorithms often require various implementation tricks and extensive hyperparameter tuning to control the instability caused by off-policy data.

On-policy policy improvement methods

the goal of monotonic policy improvement was first introduced by Kakade and Langford [14] in Conservative Policy Iteration, which maximise a lower bound on policy improvement that can be constructed using samples from the current policy.
This theory of policy improvement has served as a fundamental building block in the design of on-policy deep RL methods
to best of our knowledge, we are the first to directly relate the clipping mechanism in PPO to the total variation distance between policies

sample efficiency with off-policy data

a common approach to improving the sample efficiency of model-free reinforcement learning is to reuse samples collected under prior policies. Popular off-policy policy gradient approaches are DDPG, SAC.
these methods are not motivated by policy improvement guarantees, and do not directly control the bias introduced by off-policy data.

combining on-policy and off-policy

this is the goal of balancing the variance of on-policy methods and bias of off-policy methods
Gu et al. [10] demonstrated that the bias introduced by off-policy data is related to the KL divergence between the current policy and the behavior policy used to generate the data.
Some other methods are related to the penalty term that appears in our genralized policy improvement lower bound, which can be bounded by a penalty that depends on KL divergence

state visitation distribution

Policy improvement lower bound

we refer to the first term of the lower bound in lemma 1 as the surrogate objective, and the second term as the penalty term.
we can guarantee policy improvement at every step of the learning process by choosing the next policy $\pi_{k+1}$ to maximise this lower bound.
because the expectations in Lemma 1 depend on the current policy $\pi_k$, we can approximate this lower bound using samples generated by the current policy.

PPO why this is called proximal

it theoretically motivated by the policy improvement lower bound in Lemma 1. Rather than directly maximizing this lower bound, PPO considers the goal of maximizing the surrogate objective while constraint the next policy to be close to the current policy using CLIP
often the number of samples must be large in order for the empirical objective to be an accurate estimator for the true objective.
- because these samples must be collected under the current policy between every policy update, PPO can be very sample intensive.

Generalised policy improvement lower bound

in order to retain the stability benefits of PPO while reusing samples from prior policies, we must incorporate these off-policy samples in a principled way.
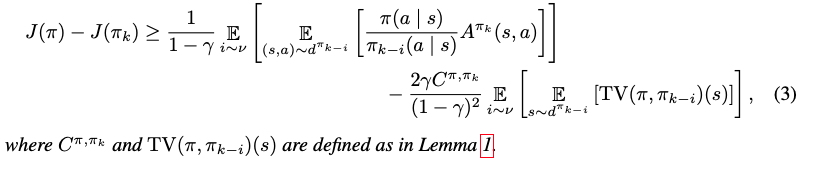
proof: we generalise Lemma 1 to depend on expectations with respect to any reference policy, and we apply this result M times for the past policies. Then, the convex combination determined by the distribution determined by $\nu$ of the resulting M policy improvement lower bounds is also a lower bound.
this lower bound provides theoretical support for extending PPO to include off-policy samples
The penalty term is Theorem 1 suggests that we should control the expected total variance distance between the future policy $\pi$ and the last $M$ policies.

this means we can effectively control the expected performance loss at every policy update by controlling the expected total variance distance between consecutive policies.
- the clipping mechanism in PPO approximately accomplish this task.

The expected total variation distance between the current policy $\pi_k$ and the future policy pi

in order to compare GePPO to PPO, we first must determine the appropriate choice of clipping parameter that results in the same worst-case expected performance loss at every update.
this shows that we must make smaller policy updates compared to PPO in terms of total variation distance, which is a result of utilizing samples from prior policies.
Assume we require N=Bn samples for the empirical objective to be a sufficiently accurate estimate of the true objective, where n is the smallest possible batch size we can collect and B is some positive integer
In this setting, PPO makes one policy update per N samples collected, while GePPO leverage data from prior policies to make B updates per N samples collected as long as M >= B.
first we see that GePPO can increase the change in total variance distance of policy throughout training compared to PPO in same training sample number.

give you some insight about how to theoretically analyse the learning efficiency