[TOC]
- Title: Compositionality as Lexical Symmetry
- Author: Ekin Akyurek; Jacob Andreas
- Publish Year: Jan 2022
- Review Date: Feb 2022
Summary of paper
Motivation
Standard deep network models lack the inductive bias needed to generalize compositionally in tasks like semantic parsing, translation, and question answering.
So, a large body of work in NLP seeks to overcome this limitation with new model architectures that enforce a compositional process of sentence interpretation.
Goal
the question of this paper aims to answer is whether compositionality like other domain-specific constraints, can be formalized in the language of symmetry.
Language symmetry
they characterise the relationship between compositionality and symmetry for general problem domains.
there comes a statement
- if a interpretation process can be computed compositionally
- e.g., query “How many yellow object in the scene” -> can be decomposed into interpreting “colour” and “objects”
- the data examples exhibits identifiable symmetries
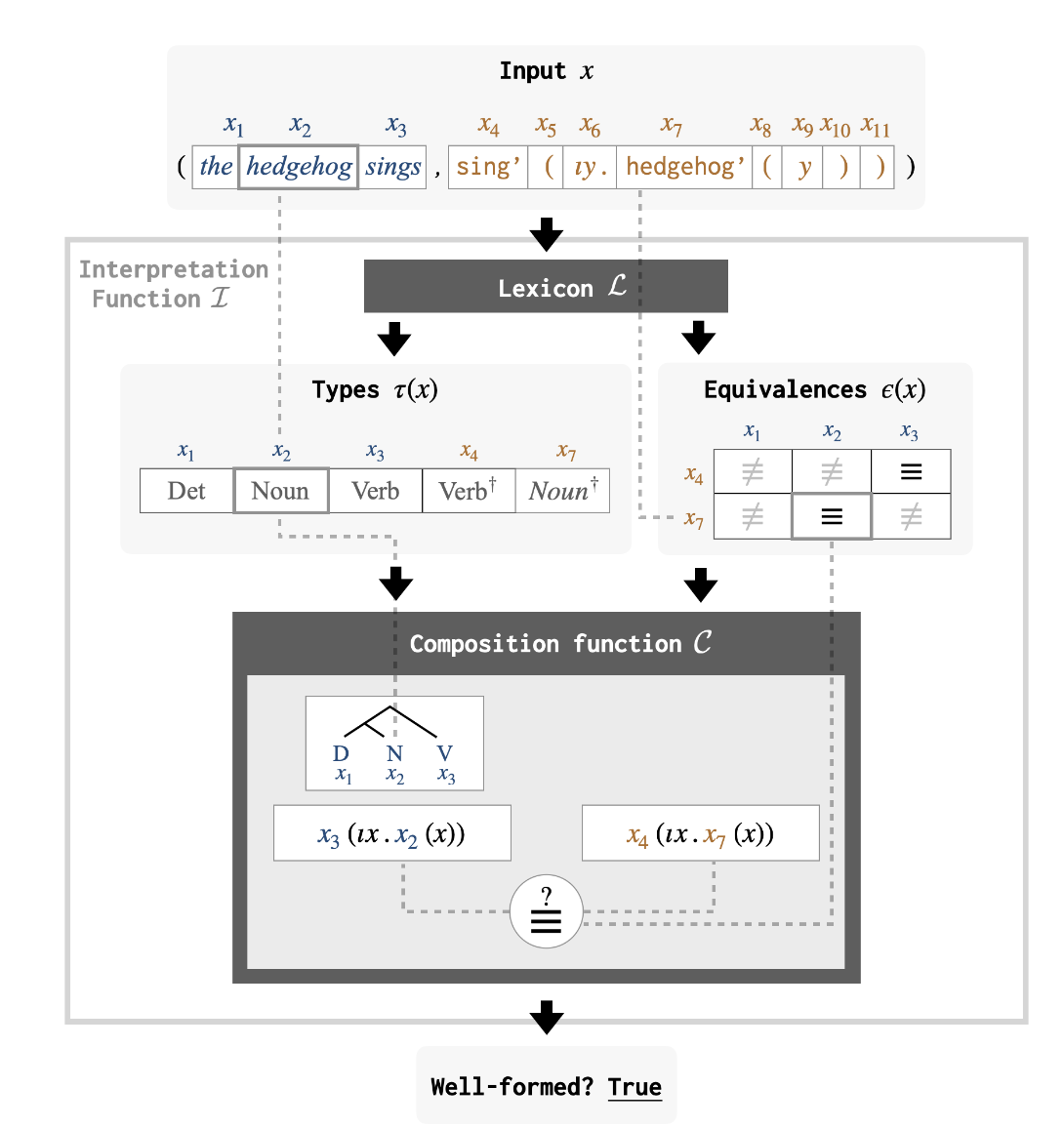
Homomorphism of symbol

Proposition
if X is L-compositional, f is an L-homomorphism and x $\in$ X, then f(x) will also $\in$ X, Thus, based on the definition of symmetry, every homomorphism of L corresponds to a symmetry of X

Alignment of text data and other-modal data pairs
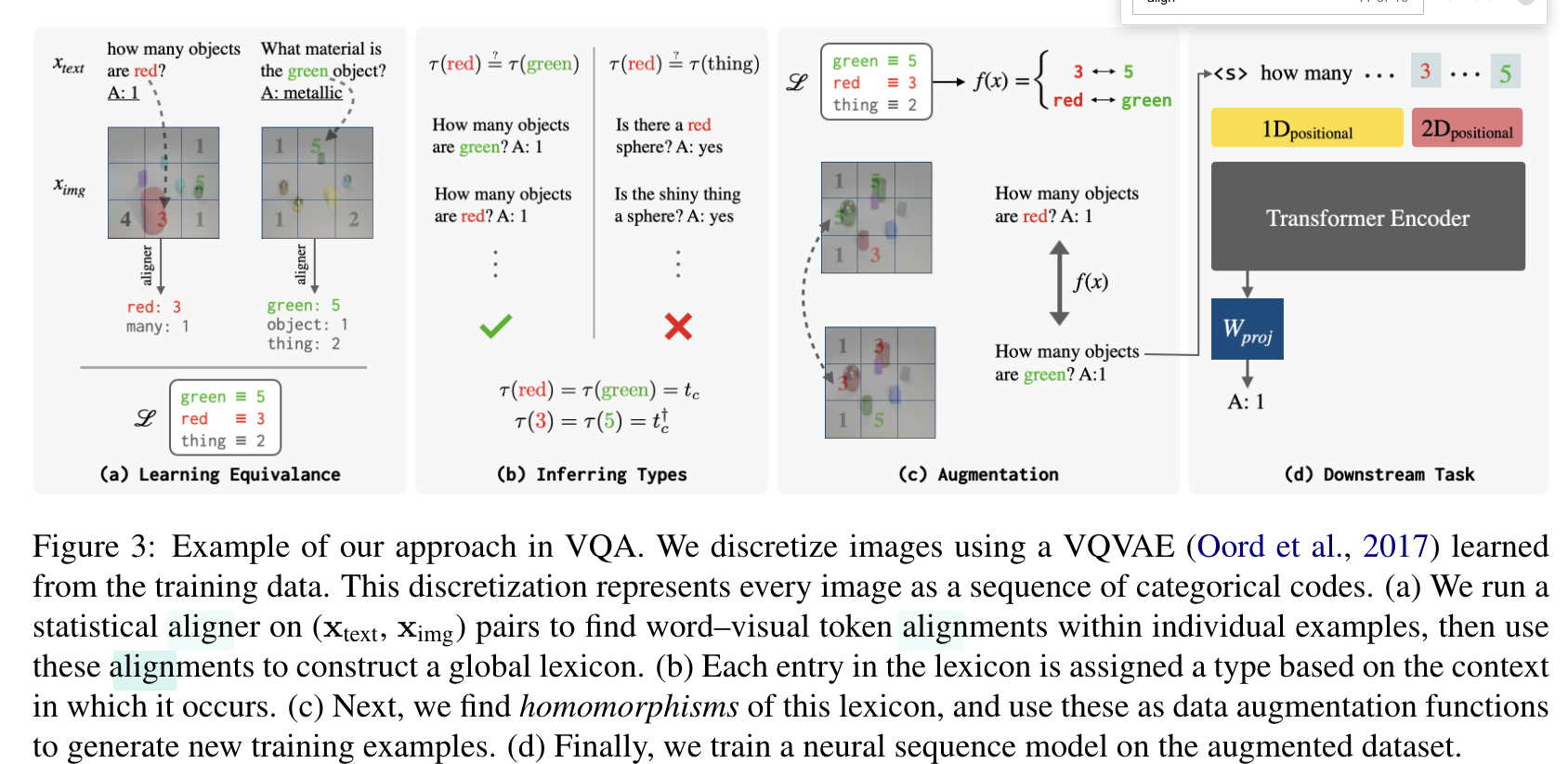
Some key terms
parameter typing schemes
TYPE is a high level module type (attention, classification, etc.)
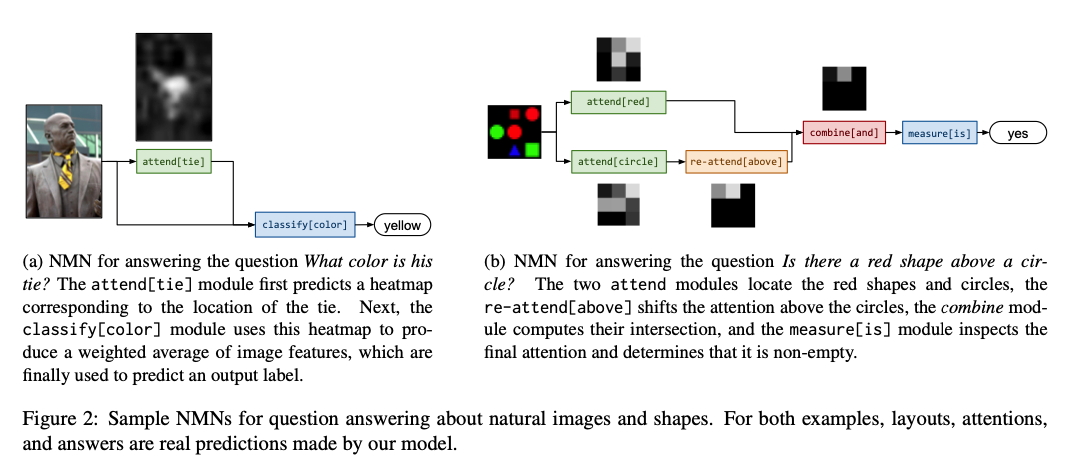
Symmetry property

Lexicon

Lexicon abstraction

Good things about the paper (one paragraph)
The author noticed that adding constraints on deep learning model architecture in order to operationalize the principle of compositionality is not effective compared to vanilla transformers.
So, the author tried to implement a data-centric view of the principle of compositionality, which means that we focus on the “transformation of a structural regularity of the lexicon” of training data so that we can capture the principle of compositionality.
Major comments
Essentially, this work gives a theoretical support for the use of data augmentation to improve generalisation performance of models.