Daniel Hierarchies of Reward Machines 2023

[TOC]

1. Title: Hierarchies of Reward Machines
2. Author: Daniel Furelos-Blanco et. al.
3. Publish Year: 4 Jun 2023
4. Review Date: Fri, Apr 12, 2024
5. url: https://arxiv.org/abs/2205.15752

Summary of paper

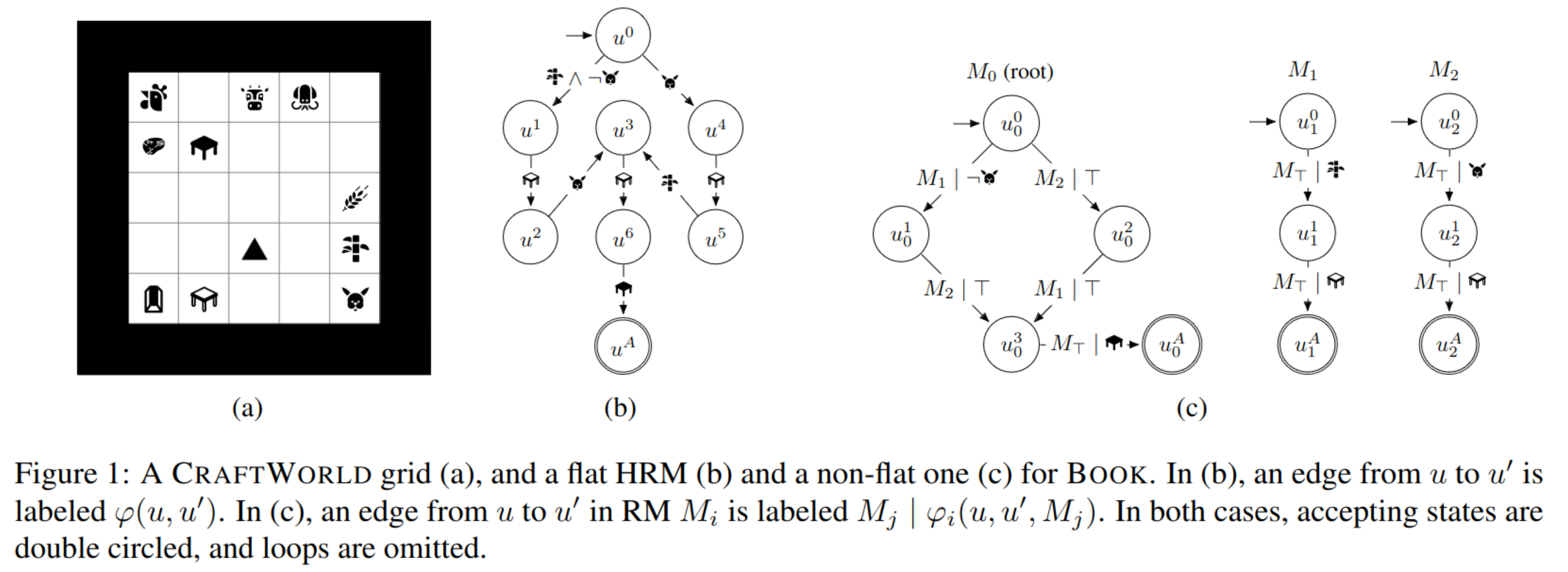
Motivation

• Finite state machine are a simple yet powerful formalism for abstractly representing temporal tasks in a structured manner.

Contribution

The work introduces Hierarchies of Reinforcement Models (HRMs) to enhance the abstraction power of existing models. Key contributions include:

1. HRM Abstraction Power: HRMs allow for the creation of hierarchies of Reinforcement Models (RMs), enabling constituent RMs to call other RMs. It’s proven that any HRM can be converted into an equivalent flat HRM with identical behavior. However, the equivalent flat HRM can have significantly more states and edges, especially under specific conditions.

2. Hierarchical Reinforcement Learning (HRL) Algorithm: A novel HRL algorithm is proposed to leverage HRMs by treating each call as a subtask. Learning policies in HRMs align with desired criteria, offering flexibility across multiple time scales and a richer range of abstract events and durations. Hierarchies also promote modularity and reusability of RMs and policies. Empirical results demonstrate that utilizing a handcrafted HRM leads to faster convergence compared to an equivalent flat HRM.

3. Curriculum-Based Learning for HRMs: A curriculum-based method is introduced to learn HRMs from traces given a set of composable tasks. This approach is essential due to the complexity of learning flat HRMs from scratch. By decomposing an RM into several simpler ones, learning becomes feasible, and previously learned RMs can efficiently explore the environment for traces in more complex tasks.

Some key terms

Reward machine

• specifically, each edge is labeled with (i) a formula over a set of high-level events that capture a task’ subgoal, and (ii) a reward for satisfying the formula
• I think each node will be the key state…
• RM fulfill the need for structuring events and durations, and keep track of the achieved and pending subgoals.

The use of HRL

• the subtask decomposition powered by HRL enables learning at multiple scales simultaneously, and ease the handling of long-horizon and sparse reward tasks.

Limitation

A common problem among methods learning minimal RMs is that they scale poorly as the number of states grows. $\rightarrow$ learning the RM automatically is an open research question

Problem Definition

label trace

$\lambda_t = \langle l(s_0), …,l(s_t)\rangle \in (2^P)^+$ assigns labels to all states in history $\langle s_0,a_0,…, s_t\rangle$

assumption: $\lambda_t, s_t$ captures all relevant information about history $h_t$ (i.e., the label trace is a summary of history state trajectory $h_t$​)

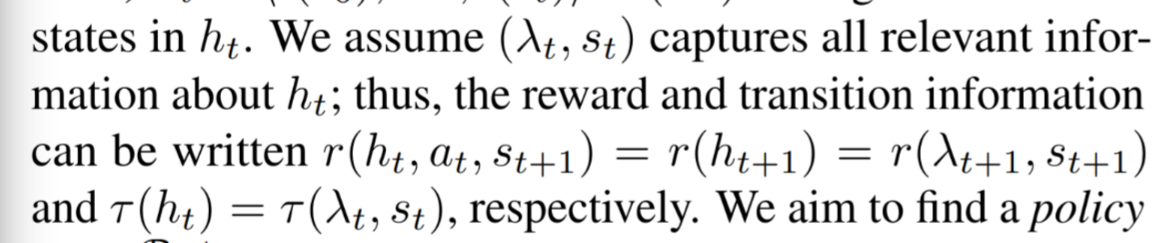
where $\tau$ is the termination function which will indicate whether a trajectory reach a terminal state or a goal state

• terminal state and goal state are different

So, we can have different types of traces

• A trace $\lambda_t$ is a goal trace if $(s^T_t, s^G_t) = (\top, \top)$,
• a dead-end trace if $(s^T_t, s^G_t) = (\top, \bot)$,
• an incomplete trace if $s^T_t = \bot$.

reward construction

• We assume that the reward is $r(\lambda_{t+1},s_{t+1})=\mathbb{1}[\tau(\lambda_{t+1},s_{t+1})=(\top,\top)]$, i.e.~$1$ for goal traces and $0$​ otherwise.

reward machine mapping to trace

Ideally, RM states should capture traces, such that (i) pairs (u, s) of an RM state and an MDP state make termination and reward Markovian, (ii) the reward r(u, u′) matches the underlying MDP’s reward, and (iii) goal traces end in an accepting state, rejecting traces end in a rejecting state, and incomplete traces do not end in accepting or rejecting states.

DNF definition

it is just the propositional logic formula

What is Disjunctive Normal Form (DNF)?

Disjunctive Normal Form (DNF) is a standard logical format used in boolean algebra where a formula is expressed as a disjunction (OR operation) of several conjunctions (AND operations) of literals. A literal is either a proposition or its negation. This form makes it straightforward to evaluate whether the formula is true based on the truth values of its constituent propositions.

Structure of a DNF Formula

A DNF formula can be structured as follows: $$ \text{DNF} = (l_{11} \land l_{12} \land \ldots \land l_{1n}) \lor (l_{21} \land l_{22} \land \ldots \land l_{2n}) \lor \ldots \lor (l_{m1} \land l_{m2} \land \ldots \land l_{mn}) $$ Where:

• $ l_{ij} $ is a literal, which can be either a proposition (e.g., $ p $) or its negation (e.g., $ \neg p $).
• Each group of literals connected by AND (e.g., $ l_{11} \land l_{12} \land \ldots \land l_{1n} $) forms a clause.
• The entire formula is a disjunction (OR) of one or more such clauses.

Examples of DNF Formulas

Here are a few examples to illustrate DNF formulas, considering a set of propositions $ P = {a, b, c} $:

1. Simple DNF Formula: $$ a \land b $$ This formula has only one clause consisting of two literals without negation.

2. Single Clause with Negations: $$ a \land \neg b $$ This formula is also a single clause but includes a negation.

3. Multiple Clauses: $$ (a \land b) \lor (\neg a \land c) $$ This DNF formula consists of two clauses. The first clause asserts that both $ a $ and $ b $ are true, while the second clause is true if $ a $ is false and $ c $ is true.

4. More Complex DNF: $$ (a \land b \land \neg c) \lor (b \land c) \lor (\neg a \land \neg b) $$ Here, the formula has three clauses with a mixture of negated and non-negated literals. It is satisfied if either both $ a $ and $ b $ are true and $ c $ is false, or $ b $ and $ c $ are both true, or both $ a $ and $ b $ are false.

Deterministic property

• the trace or we say the trajectory can only match only one transition formula
• for example, if the trace obtained both rabbit leather and paper, the reward machine will only transit from u0 to u1