Damai Dai Deepseekmoe 2024

[TOC]

1. Title: DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture of Experts Language Models
2. Author: Damai Dai et. al.
3. Publish Year: 11 Jan 2024
4. Review Date: Sat, Jun 22, 2024
5. url: https://arxiv.org/pdf/2401.06066

Summary of paper

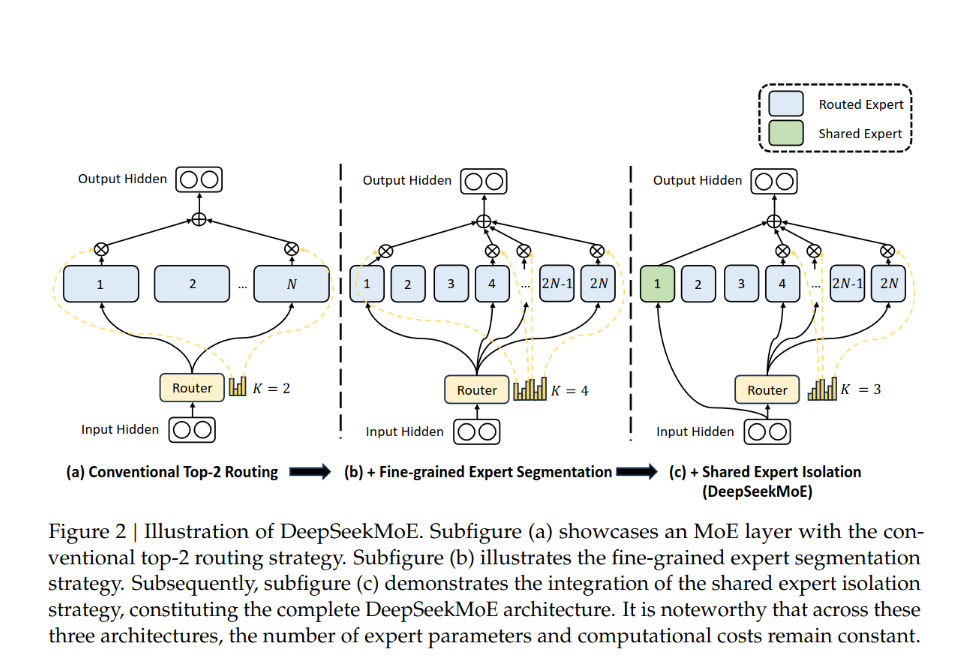
Motivation

• conventional MoE architecture like GShard, which avtivate top-k out of N experts, face challenges in ensuring expert specialization, i.e., each expert acquires non-overlapping and focused knowledge,
• in response, we propose DeepSeekMoE architecture towards ultimate expert specialization

Contribution

1. segmenting expert into mN ones and activating mK from them
2. isolating K_s, experts as shared ones, aiming at capturing common knowledge and mitigating redundancy in routed experts

Some key terms

MoE architecture

ref: [1, 2, 3, 4]

[1] R. A. Jacobs, M. I. Jordan, S. J. Nowlan, and G. E. Hinton. Adaptive mixtures of local experts. Neural Computing, 3(1):79–87, 1991. URL https://doi.org/10.1162/neco.1991.3.1. 79.

[2] M. I. Jordan and R. A. Jacobs. Hierarchical mixtures of experts and the EM algorithm. Neural Computing, 6(2):181–214, 1994. URL https://doi.org/10.1162/neco.1994.6.2.181.

[3] N. Shazeer, A. Mirhoseini, K. Maziarz, A. Davis, Q. V. Le, G. E. Hinton, and J. Dean. Outrageously large neural networks: The sparsely-gated mixture-of-experts layer. In 5th International Conference on Learning Representations, ICLR 2017. OpenReview.net, 2017. URL https: //openreview.net/forum?id=B1ckMDqlg.

[4] Dai, Damai, et al. “Deepseekmoe: Towards ultimate expert specialization in mixture-of-experts language models.” arXiv preprint arXiv:2401.06066 (2024).

Issue of existing MoE

1. knowledge hybridity
   1. limited number of experts (8), thus token will be likely to cover diverse knowledge. the expert will intend to assume vastly different types of knowledge in its parameters, which are hard to utilize simultaneously and also the expert does not focus on a single specialization but instead tries to handle a wide variety of knowledge areas
2. knowledge redundancy
   1. tokens assigned to different experts may require common knowledge. As a result, multiple experts may converge in acquiring shared knowledge in their respective parameters.

Two innovative methods

1. splitting the FFN intermediate hidden dimension

2. shared expert isolation

we isolate certain experts to serve as shared experts that are always activated, aiming at capturing and consolidating common knowledge across varying contexts.

Background

g is the gate, TopK denotes the set comprising K highest affinity score among those calculated for the t-th token and $e^l_i$​ is the centroid of the i-th expert in the l-th layer

What is $e^l_i$

In the paper it said $e^l_i$​ is the centroid of the i-th expert in the l-th layer,

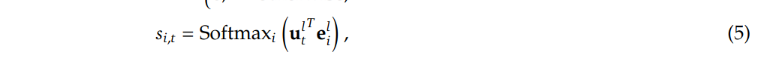
But when we see the code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class MoEGate(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.config = config
        self.top_k = config.num_experts_per_tok
        self.n_routed_experts = config.n_routed_experts

        self.scoring_func = config.scoring_func
        self.alpha = config.aux_loss_alpha
        self.seq_aux = config.seq_aux

        # topk selection algorithm
        self.norm_topk_prob = config.norm_topk_prob
        self.gating_dim = config.hidden_size
        self.weight = nn.Parameter(torch.empty((self.n_routed_experts, self.gating_dim)))
        self.reset_parameters()

    def reset_parameters(self) -> None:
        import torch.nn.init  as init
        init.kaiming_uniform_(self.weight, a=math.sqrt(5))
    
    def forward(self, hidden_states):
        bsz, seq_len, h = hidden_states.shape        
        ### compute gating score
        hidden_states = hidden_states.view(-1, h)
        logits = F.linear(hidden_states, self.weight, None)
        if self.scoring_func == 'softmax':
            scores = logits.softmax(dim=-1)
        else:
            raise NotImplementedError(f'insupportable scoring function for MoE gating: {self.scoring_func}')
        
        ### select top-k experts
        topk_weight, topk_idx = torch.topk(scores, k=self.top_k, dim=-1, sorted=False)
        

The score is calculated as

1
2
3
4

hidden_states = hidden_states.view(-1, h)
        logits = F.linear(hidden_states, self.weight, None)
        if self.scoring_func == 'softmax':
            scores = logits.softmax(dim=-1)

1
2

self.gating_dim = config.hidden_size
        self.weight = nn.Parameter(torch.empty((self.n_routed_experts, self.gating_dim)))

therefore, $e^l_i$ is actually a weight constructed and stored inside the Gate object, it is trainable also.