Alekh_agarwal on the Theory of Policy Gradient Methods Optimality Approximation and Distribution Shift 2020

[TOC]

Title: On the Theory of Policy Gradient Methods Optimality Approximation and Distribution Shift 2020
Author: Alekh Agarwal et. al.
Publish Year: 14 Oct 2020
Review Date: Wed, Dec 28, 2022

Summary of paper

little is known about even their most basic theoretical convergence properties, including: if and how fast they converge to a globally optimal solution and how they cope with approximation error due to using a restricted class of parametric policies.

One central contribution of this work is in providing approximation guarantees that are average case - which avoid explicit worst-case dependencies on the size of state space – by making a formal connection to supervised learning under distribution shift. This characterisation shows an important between estimation error, approximation error and exploration (as characterised through a precisely defined condition number)

basic theoretical convergence questions

if and how fast they converge to a globally optimal solution (say with a sufficiently rich policy class)
how they cope with approximation error due to using a restricted class of parametric policies
how they cope with approximation error their finite sample behaviour.

tabular policy parameterisation

there is one parameter per state-action pair so the policy class is complete in that it contains the optimal policy

function approximation

we have a restricted class or parametric policies which may not contain the globally optimal policy.

convergence rates (IMPORTANT)

it depends on the optimisation measure having coverage over the state space, as measured by the distribution mismatch coefficient $D_\infty$
$D_\infty$ is a measure of the coverage of this initial distribution
note that the convergence rate has no dependence on the number of states or the number of actions, nor does it depend on the distribution mismatch coefficient $D_\infty$
the convergence rate analysis uses a mirror descent style of analysis
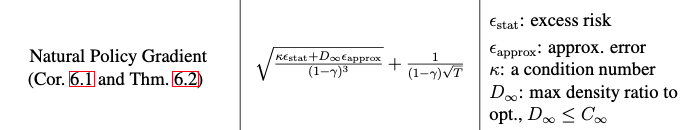
in that the worst-case density ratio only depends on the state visitation distribution of an optimal policy

excess risk

Apprixmation error

due to that the best linear fit using $w_\star^{(t)}$ may not perfectly match the Q-value.

non-stationary policy

Concentrability coefficient

Concentrability ensures that the ratio between the induced state-action distribution of any non-stationary policy and the state-action distribution in the batch data is upper bounded by a constant, called the concentrability coefficient.

overview of approximate methods

the suboptimality $V^\star (s_0) - V^\pi (s_0)$ after T iterations for various approximate algorithm, which use different notions of approximation error.
$D_\infty \leq C_\infty$ distribution mismatch coefficient is smaller than concentrability coefficient as discussed
in our policy optimisation approach, the analysis of both computational and statistical complexities are straightforward, since we can leverage known statistical and computational results from stochastic approximation literature.

The performance difference lemma

The distribution mismatch coefficient

we often characterise the difficulty of the exploration problem faced by our policy optimisation algorithms when maximising the objective $V^\pi(\mu)$ through the following notion of distribution mismatch coefficient
越大说明 explore 很差, the hardness of the exploration problem is captured through the distribution mismatch coefficient.
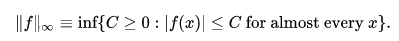
discounted state visitation distribution $d_{s_0}^\pi(s)$
Given a policy $\pi$ and measures $\rho, \mu \in \Delta(S)$, we refer to $||\frac{d_\rho^\pi}{\mu}||_\infty$, $\rho$ distribution of starting states
1. $\mu$ is fitting state distribution, (initial) state distribution

we can use this suboptimality after T iterations to prove that the PPO is slowed down by due to distribution mismatch coefficient gets harder.